Притисак

Termodinamika
Klasična Karnoova toplotna mašina
Grane Klasična termodinamika Statistička fizika
Zakoni Nulti Prvi Drugi Treći
Sistemi Termodinamičko stanje Jednačina stanja Idealni gas Realni gas Agregatno stanje Ravnoteža Procesi Izobarski Izohorski Izotermski Adijabatski Izoentropijski Izoentalpijski Kvazistatički Politropski Slobodna ekspanzija Reverzibilnost Ireverzibilnost Endoreverzibilnost Ciklusi Toplotni motori Toplotne pumpe Termalna efikasnost
Osobine sistema Termodinamički dijagrami Intenzivne i ekstenzivne veličine Funkcije stanja Temperatura / Entropija Uvod u entropiju Pritisak / Zapremina Hemijski potencijal / Broj čestica Kvalitet pare Redukovane osobine Procesne funkcije Rad Toplota
Osobine materijala Специфични топлотни капацитет  ${\displaystyle c=}$ ${\displaystyle T}$ ${\displaystyle \partial S}$ ${\displaystyle N}$ ${\displaystyle \partial T}$ Компресибилност  ${\displaystyle \beta =-}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial p}$ Термална експанзија  ${\displaystyle \alpha =}$ ${\displaystyle 1}$ ${\displaystyle \partial V}$ ${\displaystyle V}$ ${\displaystyle \partial T}$
Jednačine Karnoova teorema Klauzijusova teorema Fundamentalna relacija Jednačina stanja idealnog gasa Maksvelove jednačine Onsagerove recipročne relacije Bridgmanove termodinamičke jednačine
Potencijali Slobodna energija Slobodna entropija Unutrašnja energija ${\displaystyle U(S,V)}$ Entalpija ${\displaystyle H(S,p)=U+pV}$ Helmholcova slobodna energija ${\displaystyle A(T,V)=U-TS}$ Gibsova slobodna energija ${\displaystyle G(T,p)=H-TS}$
п р у

Притисак (тлак) је количник силе која делује нормално на површину и површине на коју сила делује нормално,^[1] што се представља формулом ${\displaystyle p={\frac {F}{S}}\,.}$ У међународном систему мерних јединица (SI) притисак се мери паскалом (Pa), који је дефинисан као сила од 1 њутна (N) по 1 m², што се представља формулом ${\displaystyle 1\,\mathrm {Pa} ={\frac {1\,\mathrm {N} }{1\,\mathrm {m^{2}} }}\,.}$ У Србији, Закон о мерним јединицама и мерилима, поред паскала допушта употребу у јавном саобраћају и јединице бар (1 bar = 100.000 Pa). Употреба ранијих јединица као што су атмосфера (1,013 · 10⁵ Pa) чија је ознака atm, висина воденог и живиног стуба (mmH₂O и mmHg) и др. није допуштена Законом.

У течностима у миру влада хидростатички притисак који зависи од дубине и једнак је тежини вертикалног стуба течности, јединичног попречног пресека, изнад посматране тачке. Делује у свим смеровима подједнако. Хидродинамички притисак се јавља у течностима у кретању и зависи од брзине течности и њене густине. Хидраулички притисак се ствара дејством спољне силе на течност и преноси се на цео систем подједнако. Притисак гаса узрокован је кретањем његових молекула и зависи од његове густине (специфичне запремине) и температуре је парцијални притисак гасова. Атмосферски притисак потиче од тежине ваздуха и одређен је тежином вертикалног стуба ваздуха над јединичном површином. Притисак паре течности: за сваку дату температуру течности у затвореном суду формира се изнад ње засићења пара под притиском који расте са температуром. Притисак светлости настаје на осветљеним телима. Сунчева светлост изазива притисак од 2 до 5 μРа у зависности од рефлексивности површине. Притисак звука на неко тело настаје под дејством звучних таласа.

Мерна јединица притиска је Паскал (знак Pa) или њутн по метру квадратном (N/m²). Осим Паскала може се употребљавати и мерна јединица притисака бар (1 bar = 10⁵ Pa). Старе јединице притисака биле су:^[2]

• техничка атмосфера, знак at (1 at = 98 066,5 Pa);^[3]
• стандардна, нормална или физичка атмосфера, знак atm (1 atm = 101 325 Pa);^[3])
• милиметар живиног стуба или милиметар стуба живе, знак mmHg, или тор (1 mmHg = 1 torr = 133,322 Pa);^[3]
• милиметар стуба воде, знак mmH₂O (1 mmH₂O = 9,806 65 Pa).

Мерне јединице за притисак

	паскал	бар	техничка атмосфера	стандардна атмосфера	тор (mmHg)	фунта силе по квадратном палцу
1 Pa	≡ 1 N/m²	= 10−5 bar	≈ 10,197×10−6 at	≈ 9,8692×10−6 atm	≈ 7,5006×10−3 torr	≈ 145,04×10−6 psi
1 bar	= 100 000 Pa	≡ 106 din/cm²	≈ 1,0197 at	≈ 0,98692 atm	≈ 750,06 torr	≈ 14,504 psi
1 at	= 98 066,5 Pa	= 0,980665 bar	≡ 1 kp/cm²	≈ 0,96784 atm	≈ 735,56 torr	≈ 14,223 psi
1 atm	= 101 325 Pa	= 1,01325 bar	≈ 1,0332 at	≡ 101 325 Pa	= 760 torr	≈ 14,696 psi
1 torr	≈ 133,322 Pa	≈ 1,3332×10−3 bar	≈ 1,3595×10−3 at	≈ 1,3158×10−3 atm	≡ 1 mmHg	≈ 19,337×10−3 psi
1 psi	≈ 6894,76 Pa	≈ 68,948×10−3 bar	≈ 70,307×10−3 at	≈ 68,046×10−3 atm	≈ 51,715 torr	≡ 1 lbf/in²

Кинетичка теорија гасова је тумачење макроскопских својстава гасова на темељу кретања њихових молекула. Основне су поставке теорије:

• молекули су најмањи делићи материје који дефинишу хемијска својства макроскопске материје;
• молекули су у сталном, хаотичном кретању (кинетичка енергија молекуларног система представља топлоту);
• међусобно деловање молекула и њихово деловање на зидове посуде у којој се гас налази може се тумачити, на бази класичне механике, као судари;
• због великог броја молекула примјенљиве су методе статистичке механике. Ако се занемари међусобно деловање молекула, говори се о идеалном гасу, за који се једноставно израчунавају темељне термодинамичке величине: притисак, температура и специфични топлотни капацитет.^[4]

Притисак гаса узрокован је ударцима молекула гаса у одређеном времену на површину зидова посуде која затвара гас. Тај је притисак то већи што је виша температура T, а мања запремина или волумен V одређене количине n гаса:

${\displaystyle p\cdot V=n\cdot R\cdot T\,}$

где је: p – апсолутни притисак гаса (Pa), V – запремина гаса (m³), n – број молова гаса, R – универзална гасна константа (8,314472 J • mol⁻¹ • K⁻¹), једнака умношку Болцманове константе и Авогадровог броја, T - апсолутна температура (у Келвинима).

Атмосферски притисак узрокован је тежином ваздуха и одређен тежином стуба ваздуха над површином.

Парцијални притисак је притисак појединих компонената у смеси гасова (Далтонов закон). притисак се може мерити као апсолутни или као релативни, према томе узима ли се за нулу вакуум или атмосферски притисак. Релативни притисак који је мањи од атмосферскога назива се негативни притисак.

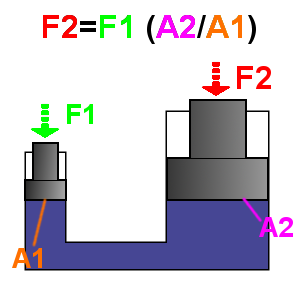
Код течности, притисак ће се јавити у два случаја:

• приликом деловања гравитације или инерцијалних сила, када ће све честице течности добити тежину те ће деловати неком укупном силом у смеру деловања резултантне силе поља у којем се течност налази. Такво деловање ће произвести хидростатички притисак;
• приликом кретања (струјања) течности, када ће на неку препреку струјању деловати сила хидродинамичког притиска, и то на површини у коју течност удара (Бернулијева једначина).

Хидростатички притисак је притисак мирног флуида, узрокован његовом тежином. Он зависи од густине флуида ρ, дубини на којој се мери h и убрзању земљине силе теже g, дакле:

${\displaystyle p=\rho \cdot g\cdot h}$

а не зависи од смера у којем се мери.

Хидраулички притисак је онај који на флуид делује споља (на пример услед деловања црпке или пумпе), а у флуиду делује једнако у свим смеровима.

Хидродинамички притисак појављује се у флуиду који струји, а састоји се од статичког и динамичког дела; потоњи зависи од брзине струјања флуида и делује у смеру струјања.

Бернулијева једначина је основни закон кретања флуида. Произлази из примене закона о очувању енергије на струјање флуида. Одатле се добије да збир:

${\displaystyle {\tfrac {1}{2}}\,\cdot \rho \ \cdot v^{2}\,+\,\rho \ \cdot g\cdot h+\,p\,=\,{\text{konstanta}}\,}$

има исту вредност свуда у флуиду који струји водоравно, где је p притисак, ρ густина и v брзина флуида у некој тачки, а h висина тежишта попречног пресека флуида у односу на неку водоравну раван. Према томе, тамо где је брзина течности већа, притисак је мањи, тамо где је брзина течности мања, притисак је већи. На Бернулијевој једначини заснивају се многе инжењерске примене, као на пример лет ваздухоплова: ваздух струји уз горњу закривљену површину крила брже него испод крила, те је притисак на доњу површину крила већи него на горњу, што има за последицу да на крила делује укупна сила према горе која диже ваздухоплов.^[5]

Кохезијски притисак се појављује само на слободној површини течности, резултат је деловања кохезијских сила.

Крвни притисак је притисак крви на зидове крвних жила. Он зависи од неколико чиниоца: од укупног обима крви што га избацује срце, о растегљивости и еластичности крвних жила, о стегнутости крвних жила. Због срчаних контракција притисак је највиши на почетку крвног оптока (у артеријама), а најнижи на његову крају, у венама. Како срце избацује крв на махове, артеријски притисак колеба између систоличке и дијастоличке вредности. У системском крвном оптоку артеријски је притисак током систоле нормално око 16 kPa (120 mm Hg), а у дијастоли око 10,5 kPa (80 mm Hg). Разлика та два притиска (5,5 kPa или 40 mm Hg) назива се притисак пулса (била). Средњи артеријски притисак нешто је ближи вредности дијастоличког притисака, јер дијастола траје дуже од систоле. У завршним деловима артеријскога система колебања притисака постају све слабијима, те је у капиларима и венама крвни притисак једнолик. На крају венскога система, на ушћу горње и доње шупље вене у десну преткомору, крвни је притисак приближно 0 kPa.^[6]

Да би се измерио притисак гаса који се налази у некој посуди, може се мерити помоћу цеви у облику слова „U” која је напуњена било којом течношћу, на пример живом. Ако је притисак гаса P_o у посуди мањи од атмосферског притисака P_a, жива ће у левом краку цеви стајати више, а у десном ниже. Да би била равнотежа у пресеку A-A, морају притисци с леве и десне стране тога пресека бити једнаки. С леве стране тога пресека делује притисак P_o и тежина стуба течности h₁. Стога је с леве стране тога пресека притисак:

${\displaystyle p_{1}=P_{o}+\rho \cdot g\cdot h_{1}}$

Притисак с десне стране пресека A-A једнак је збиру атмосферског притисака P_a и тежина стуба течности h₂, то јест:

${\displaystyle p_{2}=P_{a}+\rho \cdot g\cdot h_{2}}$

при чему је ρ - гутина течности, а g - убрзање земљине силе теже. Како вреди p₁ = p₂, то је:

${\displaystyle P_{o}+\rho \cdot g\cdot h_{1}=P_{a}+\rho \cdot g\cdot h_{2}}$

Како је очито да је h₁ - h₂ = H, добија се:

${\displaystyle \rho \cdot g\cdot H=P_{a}-P_{o}}$

У овом случају тежина стуба течности H мери разлику између атмосферског притисака и притисака у посуди. Та разлика се назива потпритисак или вакуум. потпритисак је износ за колико је притисак у некој посуди мањи од атмосферског притисака.

Када би притисак у посуди P_o био већи од атмосферског притисака, онда би сличним поступком добило да вреди:

${\displaystyle \rho \cdot g\cdot H=P_{o}-P_{a}}$

Ова разлика назива се препритисак. Препритисак је дакле износ за колико је притисак у некој посуди већи од атмосферског притиска.

Апсолутни притисак p једнак је збиру атмосферског притисака P_a и препритиска:

${\displaystyle p=P_{a}}$ + препритисак

или, апсолутни притисак p једнак је разлици атмосферског притиска P_a и подпритискa:^[7]

${\displaystyle p=P_{a}}$ - потпритисак

• Паскалов закон
• Геј-Лисаков закон
• Бојл-Мариотов закон
• Шарлов закон

• Introduction to Fluid Statics and Dynamics on Project PHYSNET
• Pressure being a scalar quantity Архивирано на сајту Wayback Machine (6. јануар 2010)